[latexpage]
zurück zu HeliHuBot Planung und Umsetzung
Training ML-Lernalgorithmen für die Klassifizierung
Mit Schwerpunkten auf:
- kurze Vorstellung eines Perceptrons und adaptive linearer Neuronen
- erster Einblick in ML-Algorithmen
Vom Neuron zum Perzeptron
Ein biologisches Neuron (Nervenzelle) ist schematisch im folgenden grob umrissen:
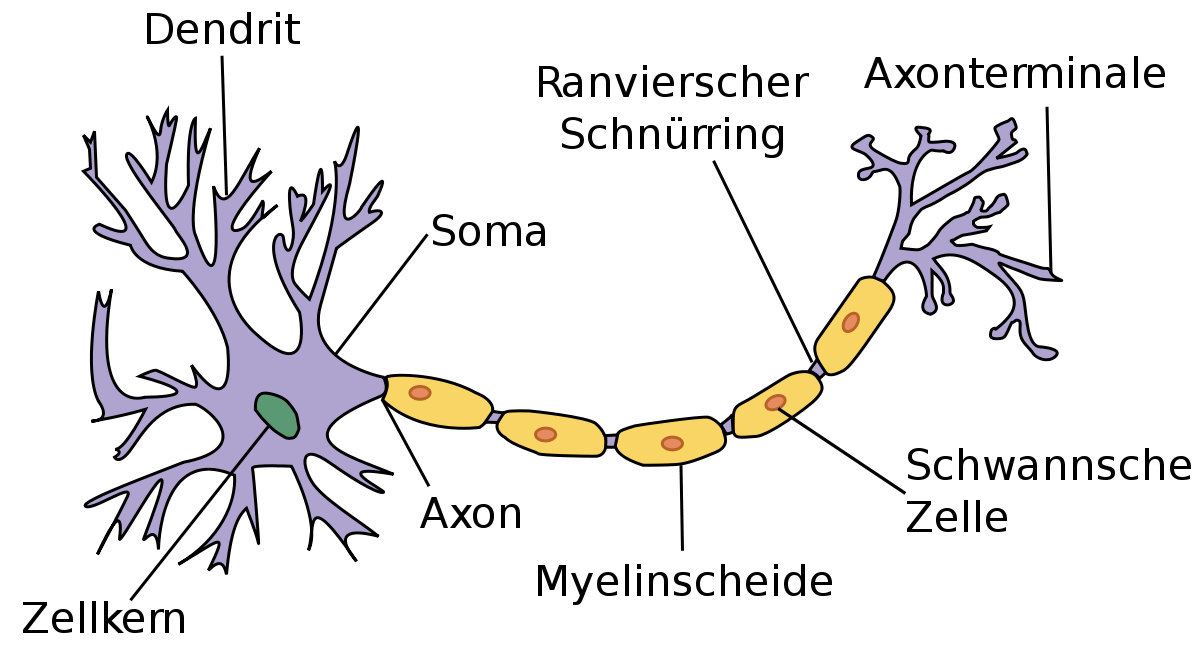
Wer sich für Details interessiert, findet welche im Kapitel I, meiner Physiologie für Biologen und Mediziner. Besonders 1) Das Ruhemembranpotential, 2) Entstehung und Fortleitung eines Aktionspotentials und 5) Synapsen kann ich als Einstieg empfehlen.
Hier werden wir nicht auf neurophysiologische Details oder auf die Vernetzung (Konnektom) eingehen, sondern wir brauchen an dieser Stelle eigentlich nur zu wissen, dass an den Dendriten Synapsen von anderen Axonenden zu finden sind (stellt den Input dar), die hemmen oder erregen können und somit das Ruhemembranpotential (RM) der Membran (Umgibt den Körper der Nervenzelle) beeinflusst. Das RM summiert sich auf und nur wenn eine bestimmte Schwelle erreicht wird (Alles oder Nichts Prinzip), entsteht ein Aktionspotential am Axonhügel (dort wo das Axon vom Körper abgeht) und breitet sich über das Axon zu den Enden aus, wo sich wieder Synapsen befinden, welche auf die nächsten Dentriten hemmend oder erregend wirken können (unser Output).
Natürlich kann ich an dieser Stelle nicht umhin, W.S. McCulloch und W. Pitts, sowie Frank Rosenblatt zu erwähnen, die Pionierarbeit auf dem Gebiet der KI leisteten, sodass 1958 das Perzeptron, das erste, sehr vereinfachte neuronales Netz, basierend auf dem McCulloch-Pitts neuron, vorgestellt werden konnte. Mit den Perzepron-Regeln konnte Rosenblatt eine Algo entwickeln, der automatisch die optimalen Gewichungskoeffizienten lernte, die dann mit den Input-Features verknüpft entschieden, ob ein Neuron feuerte (die Schwelle erreicht wurde), oder nicht. Im Kontext von supervised learning und der Klassifikation bedeutet das, dass der Algo benutzt werden konnte, um eine Zuordnung zu einer Klasse zu erreichen.
Formal können wir dieses Problem als binäre Klassifikationsaufgabe darstellen, wobei wir zur Vereinfachung unsere beiden Klassen als 1 und -1 bezeichnen. Dann können wir eine Aktivierungsfunktion definieren $latex \theta(z)$, welche eine lineare Kombination bestimmter Eingabewerte $latex \vec{x}$ und eines entsprechenden Gewichtsvektors $latex \vec{w}$ erfordert, wobei z der sogenannte net input ist z = (w1x1 + …. + wmxm):
$ \vec{w} =
\begin{bmatrix}
w\textsubscript{1} \\
\vdots \\
w\textsubscript{m}
\end{bmatrix}
$ , $ \vec{x} =
\begin{bmatrix}
x\textsubscript{1} \\
\vdots \\
x\textsubscript{m}
\end{bmatrix}
$
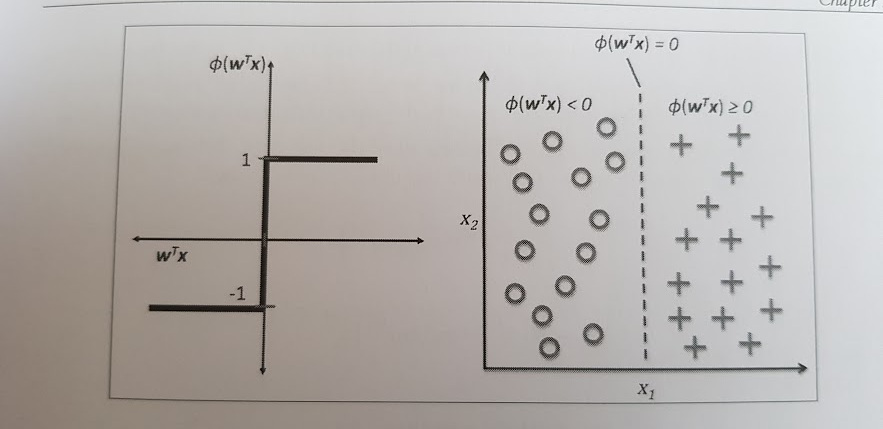
Wenn die Aktivierung eines bestimmten Beispiels x(i), also die Ausgabe von $ \theta(z)$, größer ist als ein definierter Schwellenwert $ \phi $, sagen wir Klasse 1 oder andernfalls Klasse -1 voraus.
$ \phi(z) = \biggl\{ \frac{1 if z \geq \theta}{-1 sonst}
$
Was die Notation betrifft, greife ich hier inkonsequent auf die grundlegende und oft übliche, kurze Schreibweise zurück, wie sie hier zu finden ist
Bemerkenswert ist hier, dass somit statt $\sum\nolimits_{j=0}^m$ einfach xjwj = wTx geschrieben werden kann.
Die folgende Skizze zeigt, wie der Net-Input einen binären Output ergibt und wie die Aktivierugsfunktion benutzt werden kann, um zwischen zwei linear unterscheidbaren Klassen zu unterscheiden.
Wie oben schon angemerkt, ist die Tatsache, dass ein Neuron ab einen bestimmten Schwellwert feuert im MCP-Neuron einfach umgesetzt. Rosenblatt’s Initialisierungsregel für das Perzeptron ist daher einfach zu umschreiben:
1.) Initialisiere die Gewichtung mit 0 oder kleinen zufälligen Zahlen
2.) für jedes Training, Beispiel x(i) sind die folgenden Schritte durchzuführen
a.) berechene den Ourtput-Wert ŷ
b.) aktualisiere die Gewichtung
Der Output-Wert ist hier das vorausgesagte Class-Label mittels besprochener Heaviside step function und der gleichzeitigen Aktualisierung der Gewichtung des Gewichtungsvektor wi also wi := wi + $latex \Delta$wi
$latex \Delta$wi mit dem wi aktualisiert wird, wird mit der Perceptron Lernregel berechnet $latex \Delta$wi = $latex \eta$ (y(i) – (ŷ(i))xj(i)
In dieser Lernregel ist $latex \eta$ die Lernrate (zwischen 0,0 und 1,0)
yi ist das Klass-Label und
ŷi ist das vorausgesagte Klass-Label.
Es müssen alle Gewichtungen aktualisiert werden, bevor ŷi neu berechnet wird.
$latex \Delta$w0 = $latex \eta$ (y(i) – (output(i))
$latex \Delta$w1 = $latex \eta$ (y(i) – (output(i))x1(i)
$latex \Delta$w2 = $latex \eta$ (y(i) – (output(i))x2(i) ….
Wenn das Klass-Label richtig vorausgesagt wird, bleibt die Gewichtung unverändert.
Weblinks:
https://www.cs.cmu.edu/~zkolter/course/linalg/linalg_notes.pdf von Linear Algebra Review
Weitere Quellen
Künstliche Intelligenz von Stuart Russell und Peter Norvig; ISBN 978-3-86894-098-5
Python Machine Learning von Sebastian Raschka; ISBN 978-1-78355-513-0
Neuronale Netze von Günter Daniel Rey und Karl F. Wender; ISBN 978-3-456-54881-5
