Archiv der Kategorie: Wissenswertes

Wissenswertes

4 Spannender und gesättigter Teilgraph

Schreibe einen Kommentar

zurück zu Grundbegriffe I

4 Spannender und gesättigter Teilgraph

4.1 Teilgraph

Ein Teilgraph ist ein Ausschnitt aus einem Graphen, mit einer Teilmenge an Knoten dieses Graphen, wobei maximal die Kanten vertreten sein dürfen, die auch im Graphen diese Knoten verbinden. Es kann auch ein od. mehrere isolierte Knoten vorkommen.

Def.: Ein Graph X1 = (V1,E1) heißt Teilgraph von X = (V,E), wenn V1 ⊆ V und E1 ⊆ E ist.

4.2 Spannender Teilgraph

Besitzt alle Knoten des Graphen, aber nicht alle der Kanten, die diese Knoten verbinden, wie im Graphen.

Ein Teilgraph X1 von X ist ein spannender Teilgraph von X, wenn V1 = V ist.

4.3 Gesättigter Teilgraph

Teilgraph herausgeschnitten aus Graph, Knoten und alle seine Kanten, mit denen sie untereinander verbunden sind.

Äußere Knoten und deren inzidente Kanten fallen weg.

Def.: Enthält E1 alle Kanten aus E, deren Endpunkte in V1 liegen, so sagt man, dass X1 von V1 ⊆ V in X aufgespannt wird, oder dass X1 ein gesättigter Teilgraph von X ist.

4.3.1 Spannender, gesättigter Teilgraph

Ein Teilgraph ist der Graph selbst, da eine Menge seine Teilmenge sein kann.

V1 = V2

V1 = V

gesättigt + spannend = derselbe Graph ≠ der gleiche Graph

nach oben

Wissenswertes

3 Isomorphie von Graphen

Ein Kommentar

zurück zu Grundbegriffe I

Grundbegriffe I

3 Isomorphie von Graphen

Unterschiedliche Graphen (z.B. bei anderer Bezeichnung der Knoten) können die gleiche Struktur und Abbildung aufweisen.

* Definition: Gegeben seien X1 = (V1,E1) und X2 = (V2,E2)
Eine bijektive Abbildung φ: V1→V2 heißt ein ISOMORPHISMUS von X1 auf X2, wenn gilt: [x,y] ⇔ [φ(x), φ(y)] ∈ E2; X1 ≈ X2

3.1 Eigenschaften fon Abbildungen

Die Abbildung f:X→Y kann folgende Eigenschaften haben:

  • injektiv: x1∧y2(x1 ≠ x2 → f(x1) ≠ f(x2)) |B| ≥ |A|

    jedes Element der Urmenge wird genau einmal in der Zielmenge abgebildet, wobei Elemente in der Zielmenge möglich sind die kein Urbild haben;
  • surjektiv: x∧y∨(f(x)=y) |B| ≤ |A|
    jedes Element der Urmenge wird einmal oder öfter in der Zielmenge abgebildet, wobei Elemente in der Zielmenge ohne Urbild nicht möglich sind;
  • bijektiv: a ∧ b |B| = |A|
    Jedes Element der Zielmenge hat genau ein Urbild und umgekehrt, d.h. bijektiv ist injektiv verknüpft mit surjektiv z.B.:
    φ (a ◦ b) = φ (a) ∧ φ (b) → φ (a * b) = φ (a) + φ (b)
    log (a*b) = log (a) + log (b)

    f:x→y
    3Isomo1
    3Isomorphie1

    operationentreue Abbildung
    z.B.: log(a*b) = log a + log b
    bijektive Abbildung der Elemente und der Funktionen
    p ∧ q ⇔ ¬( ¬p v ¬q)
    Entsprechungen:
    ∩∪’
    ∧∨¬
    3Isomorphie1

  • isomorph
    (bijektiv + strukturerhaltende Abbildung)
    Urbildmenge – Bildmenge:

    • Gleiche Anzahl von Elementen (Knoten u. Kanten)

    • Gleicher Knotengrad

    • Strukturerhaltung, Nachbarschaften (Abbildungen können unterschiedlich sein)

    Bijektive Abblidung zwischen 2er Graphen:

    1. 1.Abbildung muß umkehrbar eindeutig sein

    2. 1.wenn ein Knoten im 1. Graphen existiert, genau dann muß er auch im 2. Graphen existieren

3.2 Vorraussetzung

Die Anzahl der Knoten, Knotengrade und Kanten ist gleich.

3Isomo20

Der gleiche Graph und doch nicht der selbe (gleiche Struktur). Wegen bijektiver Abb. folgt, daß die gleiche Anzahl an Knoten vorhanden sein müssen.

3Isomo7

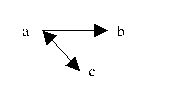
x            y            z

3Isomo8

X ≈ Y
X und Y sind isomorph.

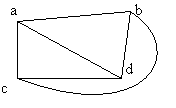
Beispiel 2:
X1 = ({1,2,3,4,5,6,7}, {[1,2],[1,4],[1,5],[2,3],[2,6],[3,4],[3,7],[4,5],[5,6],[5,7],[6,7]})
X2=({A,B,C,D,E,F,G},[G,F],[E,F],[G,D],[D,E],[C,F],[E,B],[B,C],[A,G], A,D],[A,C],[A,B]})

3Isomo10

Der Knoten 5 bzw. A hat den Grad 4.

Permutation – wenn Nachbarschaftsbeziehungen bekannt sind kann nähere Auswahl getroffen werden.
.) Knoten betrachten die bes. Grad aufweisen.
.) Knoten mit best. Grad müssen gleich sein.
.) Knoten mit bes. Grad suchen und dann die Nachbarschaftsbeziehungen feststellen.
Tabelle:

1 D G D G
2 E E F F
3 F F E E
4 G D G D
5 A A A A
6 B B C C
7 C C B B

Aufgabe:

3Isomo13

3Isomo12

3Isomo11
3Isomo12
3Isomo13

a
b k k
c j l
d
e
f
g o o
h

daher: X¬≅Y

a u
b t
c s
d r
e q
f x
g w
h v

daher: X≅Z
→ Z¬≅Y

weiteres Beispiel zur Isomorphie:

3Isomo14
3Isomo15

Bei isomorphen Graphen gilt, dass für alle Verknüpfungen der Urbildmenge auch die Verknüpfungen der Bildmenge dasselbe Ergebnis ergeben.

3.2.1 Notwendige Bedingungen für Isomorphismus

  1. Anzahl Kanten gleich
  2. Anzahl Knoten gleich
  3. gleicher Knotengrad

Diese Bedingungen sind notwendig, aber noch nicht hinreichend für einen Isomorphismus.

3.2.2 Algrorithmus für Feststellung von Isomorphismus

  1. beginnend bei einem, aufgrund seines Knotengrades, eindeutigen Knoten, abbilden
  2. fortsetzend, unter Einhaltung der Nachbarschaftsbeziehung, abbilden
  3. Lösung von Isomorphismus mit kurzen Stichworten beschreiben
  4. wenn ein Graph x nicht isomorph mit einem von 2 miteinander isomorphen Graphen ist, so kann er es auch nicht mit dem 2. Graphen sein

3Isomo16

3.2.3 Adjazenzmatrix A(x) (Nachbarschaftsmatrix)

3Isomo17
wenn der Knoten i mit dem Knoten j über eine Kante verbunden ist, dann erfolgt der Eintrag 1 ansonst 0.

Bei der Adjazenzmatrix-Darstellung werden die Knoten als Indexwerte einer 2-dimensionalen Matrix A aufgefasst.
Wenn der Knoten v adjazent zum Knoten w ist, wird das Feld A[v,w] in der Matrix gesetzt (z.B. 1 als “true-Wert”, etc.).
Die Adjazenzmatrix ist:

  • gut für kleine Graphen oder Graphen mit vielen Kanten
  • gut für die Überprüfung von Adjazenzeigenschaft
  • dfs schlecht, Rechenaufwand O(|V|2)
  • quadratischer Speicheraufwand O(|V|2)

3.2.4 Verschiedene Matrizenformen und deren Bedeutung

Hauptdiagonale 0 – Graph weist keine Schlingen auf
Hauptdiagonale 1 – von einem Knoten kommt man über eine spezielle Kante wieder auf den selben Knoten
Symetrische Matrix – wenn die Matrix über die Hauptdiagonale gespiegelt werden kann, handelt es sich um einen ungerichteten Graphen
Asymetrische Matrix – es liegt ein gerichteter Graph vor

3.2.5 Anordnung und Prüfung auf Isomorphismus zweier Matrizen

  1. ordnen beider Matrizen nach Knotengrad der Knoten, höchste Knotengrade zuerst
  2. prüfen ob Isomorphismus nachgewiesen werden kann und ausgeben wenn Isomorphismus besteht
  3. vertauschen der Indizes (gleichweiser Spalten- u. Zeilentausch) der 2. Matrix innerhalb der Knotengrade
  4. inklusive der letzten möglichen Vertauschung, weiter bei Pkt. 2, ansonst ENDE
A(x) A B C D E F
A 0 1 0 0 0 0
B 1 0 1 0 0 0
C 0 1 0 1 0 0
D 0 0 1 0 1 1
E 0 0 0 1 0 0
F 0 0 0 1 0 0
A(z) M N O P Q R
M 0 1 0 0 0 0
N 1 0 1 1 0 0
O 1 0 0 0 0 0
P 0 1 0 0 1 0
Q 0 0 0 1 0 1
R 0 0 0 0 1 0

Der Index der Matrix A(z) wird nun solange vertauxcht, bis alle Möglichkeiten ausgeschöpft sind.

A2(z) M N O P Q R
M 0 0 0 1 0 0
N 0 0 0 1 1 0
O 0 0 0 1 0 0
P 1 1 1 0 0 0
Q 0 1 0 0 0 1
R 0 0 0 0 1 0

3.2.6 Mehrfach-ISOMORPHISMUS

Mehrfach-Isomorphismus liegt dann vor, wenn mehrere Graphen
eindeutig umkehrbar abbildbar sind.

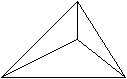
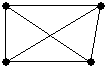
Die beiden Graphen scheinen sehr unterschiedlich zu sein,
dennoch sind sie im Sinne der Graphentheorie strukturgleich. Man kann bijektive
Abb. der Eckenmenge angegeben, die die Inzidenzbeziehungen
respektiert. Man spricht von isomorphen Graphen. Das top. Bild eines top.
Graphen führt stets zu einem isomorphen Graphen.

3Isomo19

3Isomo18
3Isomo19

nach oben

Wissenswertes

2. Unterteilung der Graphen

Schreibe einen Kommentar

zurück zu Grundbegriffe I

2.1 Unterteilung der einfachen Graphen

2.1.1 Einfache, schlichte Graphen

Das sind Graphen ohne Schlingen (Kante von einem Knoten zu sich selbst) und ohne Mehrfachkanten.

X1 = ({a, b, c, d}, {[a, b], [a, c], [a, d], [b, c], [b, d], [c, d]})
Ist ein ungerichteter Graph, welcher mit unterschiedlichen Darstellungsmöglichkeiten gezeichnet werden kann.

X2 = (V2, E2)
V2 = {A, B, C, D}
E2 = {[A, B], [A, C], [A, D], [B, C], [B, D], [C, D]}
Ist ebenfalls ein ungerichteter Graph, welcher mit denselben Darstellungsmöglichkeiten gezeichnet werden kann, nur die Knotenbezeichnung ist anders. Struktur (Beziehung zwischen den Komponenten) ist gleich. Daher können unterschiedliche Graphen eine gleiche Abblidungen haben.

2.1.2 Ungerichteter Graph

X(V,E); jeder Kante entspricht ein ungeordnetes Paar von Knoten, das in eckige Klammern gesetzt wird; e ∈ E(X) und x,y ∈ V(X); e ⇒ [x,y]; x y

Def: Graph X = (V,E)
V…(endl.) Menge von Knoten
E…(endl.) Menge von Kanten
[x,y]… ungerichtete Kante zwischen x und y

2.1.3 Gerichteter Graph

jeder Kante entspricht ein geordnetes Paar von Knoten, das in spitze Kalammern gesetzt wird:e ∈ ⟨x,y⟩ x ⇒ y; ⟨y,x⟩ x ⇐ y;

2.1.4 Gemischte Graphen

es treten geordnete und ungeordnete Paare auf.

2.1.5 Plättbarer Graph

z.B. einschichtige Platine

plättbare Graphen lassen sich als Strecken darstellen z.B.:

V(x)= {} E(x)= {}

x = ({a,b,c,d},{[a,b],[a,c],[a,d],[b,c],[d,b]}

*********************

adjazent (anliegend) bedeutet: zwei Knoten (Kanten) sind benachbart!

(nur innerhalb desselben Typs, also Kante-Kante oder Knoten-Knoten)

inzident bedeutet: Knoten ist Bestandteil der Kante! (bei unterschiedlichen Typen)

Vergleich: Kohäsion und Adhäsion

Bei gerichteten Graphen spricht man auch von Nachfolger; bei ungerichteten Graphen von Nachbar.

Wissenswertes

1. Definition, Anwendungen, Darstellung

Schreibe einen Kommentar

zurück zu Grundbegriffe I

1.1 Definition eines Graph

Def.: Ein Graph G ist ein Paar (V,E) zweier endlicher Mengen – Menge 1 ist V (G), die Menge der Knoten (-punkte) und Menge 2 ist E(G), die Menge der Kanten, wobei jedem Element der Menge E(G) ein (un-) geordnetes Paar aus V(G) zugeordnet ist.

1.1.1 Zur Entstehung

Die Graphentheorie ist übrigens der Mathematik zugehörig und bedient sich der Notation der Mengenlehre.

Die Wurzel der Graphentheorie liegt in der Untersuchung topischer Probleme, die sich durch eine Anzahl von Ecken (Punkten) und Kanten (Verbindungen) zwischen ihnen geschreiben lassen. Beispiel ist das Königsberger Brückenproblem (siehe unter Euler’sche Linie).

1.2 Anwendung

Mit Graphen können Strukturen, Hirachien, Abläufe und dergleichen dargestellt und untersucht werden.

Z.B.: alle möglichen Netze (Verkehrs-, Telefonnetz…), Baumstruktur, Flußdiagramm, Organigramme, Netzpläne für Programmabläufe, Datenstrukturen, endl. Automaten, Organisationsformen Netzwerke…
Besonders in der Informatik lassen sich durch Graphen viele Probleme beschreiben und über Graphenalgorithmen lösen.

Die endlichen Graphen der Graphentheorie können wie folgt dargestellt werden:

  • Straßennetz: Kreuzungen = Knoten und Straßen = Kanten
  • Schaltnetze: Schalter bzw. Gatter = Knoten und Leitung = Kante
  • Computernetwerk: Computer = Knoten und Verbindungskabel = Kante…

Ein Funktionsgraph aus der Mathematik hat hingegen unendlich viele Knoten:

Siehe auch GEDV: formale Sprachen; Syntax Homomorphismus; endlicher Automaten

1.3 Darstellung von Graphen

X= (V,E)

V steht für Vertex = Knoten

E für Edge = Kante

V und E sind Mengen mit endlich vielen Elementen;

  • Aufzählung der Elemente V={1,2,3}
  • Beschreibung
  • graphische Darstellung (nur bei kleinen Graphen möglich)

1.4 Speicherung von Graphen

2 Methoden zur Speicherung von Graphen: Adjazenzmatrix-Darstellung und Adjazenzlisten-Darstellung.
Ein Knoten v heißt adjazent zu einem Knoten w, wenn eine Kante von v nach w führt.

Wissenswertes

Memristor als technisches Neuron?

Schreibe einen Kommentar

Memristoren sind wirklich eine geniale, viel vewrsprechende Erfindung. Auf Lernfähige Memristoren fragt man sich, ob sie die Keimzellen für künstliche Menschen sind.
Zitat aus dem Artikel von Michael Engel:

Dank seiner Memristoren, die das alles quasi “von klein auf” lernen – vergleichbar mit Neugeborenen, deren Nervenzellen im Gehirn auch noch nichts von der Welt wissen, in die sie hineinwachsen.

Sind Memristoren die Keimzelle für die Entwicklung einer künstlichen Intelligenz, letztlich sogar die Keimzelle künstlicher Menschen, die sich eines Tages freuen können, fühlen und leiden wie wir?


Memistor auf Wikipedia:

Ein Memristor – der Name ist ein Kofferwort aus memory (Speicher) und resistor (elektrischer Widerstand) – ist ein passives elektrisches Bauelement, dessen elektrischer Widerstand nicht konstant ist, sondern von seiner Vergangenheit abhängt. Der aktuelle Widerstand dieses Bauelements ist davon abhängig, wie viele Ladungen in welcher Richtung geflossen sind. Damit ist der Widerstandswert über den zeitlichen Verlauf des geflossenen Stroms einstellbar. Dieser Widerstand bleibt auch ohne Energiezufuhr erhalten.

Memristoren werden manchmal neben dem Widerstand, dem Kondensator und der Spule als viertes fundamentales passives Bauelement beschrieben.

Weblinks:
memristor.org
Demystifying the memristor
Scientists Create First Memristor: Missing Fourth Electronic Circuit Element
Scientists Create First Memristor: Missing Fourth Electronic Circuit Element
Memristoren imitieren die „grauen Zellen“
Strom aus, Speicher an
Hoffnungsträger Memristor
Neue Speicher-Chips mit Memristor-Technik?

Bildquellen:
Wikipedia Bild 1: Urheber J. J. Yang, HP Labs. und Bild 2: Michael Lenz